הבדלים בין גרסאות בדף "שיחה:88-132 סמסטר א' תשעא"
(←הוכחת אינדוקציה) |
(←עזרה בפתרון שאלה: תיקון מיקום חדר מחלקה) |
||
| שורה 162: | שורה 162: | ||
איפה זה חדר מחלקה שבו יתקיים שיעור חזרה ביום חמישי הקרוב?? | איפה זה חדר מחלקה שבו יתקיים שיעור חזרה ביום חמישי הקרוב?? | ||
:{{לא מתרגל}}<math>\lim_{k\to\infty} a_{n_{k+1} }-a_{n_k}=0</math> ולכן <math>\forall\varepsilon>0:\ \exists k_0\in\mathbb N:\ \forall k>k_0:\ |a_{n_{k+1} }-a_{n_k}|<\varepsilon</math>. זה נכון לכל תת סדרה של <math>\{a_n\}</math>, כלומר לכל סדרה טבעית עולה ממש <math>\{n_k\}</math>. לכן לכל m,n כך ש-m>n (בה"כ) נבחר סדרה <math>\{n_k\}</math> המקיימת <math>\exists k\in\mathbb N:\ n_k=n\and n_{k+1}=m</math> ולכן <math>\forall\varepsilon>0:\ \exists n_0\in\mathbb N:\ \forall n\ne m\and n,m>n_0:\ \vert a_m-a_n\vert<\varepsilon</math>. אם m=n אז <math>|a_m-a_n|=0<\varepsilon</math> ולכן סדרת קושי. {{משל}} | :{{לא מתרגל}}<math>\lim_{k\to\infty} a_{n_{k+1} }-a_{n_k}=0</math> ולכן <math>\forall\varepsilon>0:\ \exists k_0\in\mathbb N:\ \forall k>k_0:\ |a_{n_{k+1} }-a_{n_k}|<\varepsilon</math>. זה נכון לכל תת סדרה של <math>\{a_n\}</math>, כלומר לכל סדרה טבעית עולה ממש <math>\{n_k\}</math>. לכן לכל m,n כך ש-m>n (בה"כ) נבחר סדרה <math>\{n_k\}</math> המקיימת <math>\exists k\in\mathbb N:\ n_k=n\and n_{k+1}=m</math> ולכן <math>\forall\varepsilon>0:\ \exists n_0\in\mathbb N:\ \forall n\ne m\and n,m>n_0:\ \vert a_m-a_n\vert<\varepsilon</math>. אם m=n אז <math>|a_m-a_n|=0<\varepsilon</math> ולכן סדרת קושי. {{משל}} | ||
| − | :בקשר לחדר המחלקה, הוא נמצא בבניין | + | :בקשר לחדר המחלקה, הוא נמצא בבניין 216 בחדר בקומה השנייה וכתוב על הדלת "חדר סטודנטים" (לא זוכר מה המספר). |
::(לא אני שאלתי על החדר המחלקה, יש לשים את זה בכותרת נפרדת). אני לא בטוח שהפתרון הזה נכון, מכיוון שאני חושב שבפתרון הזה ה n0 תלוי ב-m ו-n, ואסור שתהיה תלות. תקנו אותי אם אני טועה? | ::(לא אני שאלתי על החדר המחלקה, יש לשים את זה בכותרת נפרדת). אני לא בטוח שהפתרון הזה נכון, מכיוון שאני חושב שבפתרון הזה ה n0 תלוי ב-m ו-n, ואסור שתהיה תלות. תקנו אותי אם אני טועה? | ||
גרסה מ־19:10, 25 בינואר 2011
תוכן עניינים
הוספת שאלה חדשה
הוסף שאלה חדשה (רשום כותרת לשאלה, רשום את תוכן השאלה ולחץ על שמירה למטה מימין לסיום).
-עזרה על עיצוב הטקסט וכתיב מתמטי תוכלו למצוא כאן
אם אתם רוצים לשאול שאלה עליכם ליצור חשבון משתמש באתר.
ארכיון
- ארכיון 1
- ארכיון 2
- ארכיון 3
- ארכיון 4
- ארכיון 5
- ארכיון 6
- ארכיון 7
- ארכיון 8
- ארכיון 9
- ארכיון 10
- ארכיון 11
- ארכיון 12
- ארכיון 13
- ארכיון 14
שאלות
שאלה על פתרון לתרגיל
http://math-wiki.com/images/b/b5/10Infi1Targil11Sol.pdf פה, תרגיל 11, בשאלה 1, כתבת:
"כפי שראינו בכיתה, ניתן להשלים את f לפונקציה רציפה בקטע הסגור a M [ , 1] ולכן היא רציפה שם במ"ש". תוכל להרחיב בנושא? ניתן להוכיח את התרגיל בלי לעשות טריקים כאלה של השלמה?
וגם, בקטע עם דלתא, כתבת "ניתן לבחור 1>ל>0". למה? איך יודעים מהו דלתא? וגם למה צריך את זה? אפשר להוכיח את הקטע הזה בדרך אחרת ע"י השימוש בזה שהגבול בa מימין קיים, ולהראות ש-f רציפה במ"ש ב ![(a,M]](/images/math/4/0/a/40a2ba2d0a20ad56b298c7e3bd10c4ad.png) ?
?
- יש לה אי רציפות סליקה בa ולכן ההשלמה הזו זה סילוק אי הרציפות על ידי הגדרת הערך של הפונקציה בa להיות הגבול שם מימין. לגבי הדלתא, אם משהו נכון עבור דלתא גדול מאחד, הוא בוודאי נכון לכל דלתא קטן מאחד. אנחנו עושים את זה על מנת שלא יצאו לנו שתי נקודות כך שאחת בקטע האינסופי ואחת בקטע הסופי (לכן יש חפיפה בינהם). --ארז שיינר 19:24, 24 בינואר 2011 (IST)
- כמה שאלות: -למה לפונקציה אי רציפות סליקה בa? למה אם משהו נכון עבור דלתא גדול מאחד, הוא נכון גם לדלתא קטן מיוחד (כפי שאני רואה את זה- אם x<d=2 אז לא בהכרח x<1)? -בשביל מה הקטע החופף? בשביל שיהיה "אותו דלתא" גם אם x שייך לקטע האינסופי וגם לסופי? אבל בקטע האינסופי אין בכלל דלתא! תודה.
- כי יש לה גבול סופי בa זו ההגדרה של אי רציפות סליקה. אמנם זה חד צדדי, אבל זה מספיק כי זה קצה הקטע (פונקציה רציפה ב[a,b] אם היא רציפה בקטע הפתוח וקיימים לה הגבולות החד צדיים בקצות הקטע ושווים לערך הפונקציה שם). הכוונה היא שאם קיים דלתא (נניח 2) כך שלכל איקס שקרוב לאיקס אפס עד כדי דלתא משהו קורה, בפרט המשהו הזה קורה לכל איקס שקרוב לאיקס אפס עד כדי דלתא קטן יותר (נגיד אחד) כי זה אפילו קרוב יותר. יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם. --ארז שיינר 20:09, 24 בינואר 2011 (IST)
- 2 דברים- לא הבנתי את הקטע של עד כדי דלתא, בד"כ (בפרט בהוכחה של רציפות במ"ש צריך להוכיח שאם משהו (ברציפות במ"ש |x1-x2|<דלתא) אז קורה משהו (..קטן מאפסילון) ופה אם משהו נכון לדלתא כלשהו הוא לא בהכרח נכון לדלתא קטן יותר (אז לא הבנתי נכון את הכוונה). דבר שני, לגבי יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם"- אבל בפועל כן יכולים להיות 2 איקסים שאחד בקטע ובשני לא, אז אם ההוכחה לא תקפה לגביהם, היא לא נכונה עבורם- ואז לא נכונה תמיד?
- בגלל שדלתא קטן מאחד, לא יכולים להיות שני איקסים במרחק אחד שלא מוכלים שניהם באחד הקטעים. לגבי הדלתא: אם לכל
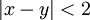 מתקיים
מתקיים 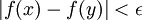 בוודאי נכון לומר שלכל
בוודאי נכון לומר שלכל 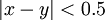 מתקיים
מתקיים 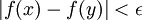 . --ארז שיינר 21:32, 24 בינואר 2011 (IST)
. --ארז שיינר 21:32, 24 בינואר 2011 (IST)
- בגלל שדלתא קטן מאחד, לא יכולים להיות שני איקסים במרחק אחד שלא מוכלים שניהם באחד הקטעים. לגבי הדלתא: אם לכל
- 2 דברים- לא הבנתי את הקטע של עד כדי דלתא, בד"כ (בפרט בהוכחה של רציפות במ"ש צריך להוכיח שאם משהו (ברציפות במ"ש |x1-x2|<דלתא) אז קורה משהו (..קטן מאפסילון) ופה אם משהו נכון לדלתא כלשהו הוא לא בהכרח נכון לדלתא קטן יותר (אז לא הבנתי נכון את הכוונה). דבר שני, לגבי יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם"- אבל בפועל כן יכולים להיות 2 איקסים שאחד בקטע ובשני לא, אז אם ההוכחה לא תקפה לגביהם, היא לא נכונה עבורם- ואז לא נכונה תמיד?
- כי יש לה גבול סופי בa זו ההגדרה של אי רציפות סליקה. אמנם זה חד צדדי, אבל זה מספיק כי זה קצה הקטע (פונקציה רציפה ב[a,b] אם היא רציפה בקטע הפתוח וקיימים לה הגבולות החד צדיים בקצות הקטע ושווים לערך הפונקציה שם). הכוונה היא שאם קיים דלתא (נניח 2) כך שלכל איקס שקרוב לאיקס אפס עד כדי דלתא משהו קורה, בפרט המשהו הזה קורה לכל איקס שקרוב לאיקס אפס עד כדי דלתא קטן יותר (נגיד אחד) כי זה אפילו קרוב יותר. יש חפיפה על מנת שלא יהיו x_1,x_2 כך שאחד מהם בקטע אחד והשני בקטע השני ואז ההוכחה לא תהיה תקיפה לגביהם. --ארז שיינר 20:09, 24 בינואר 2011 (IST)
שאלה קודמת (טור)
עדיין לא הבנתי פתרון לשאלה ששאלתי וכעת שייכת לארכיון - [[1]] תודה!
- אני לא יודע מה הקשר לקטן או גדול זה עניין של גבול. אם
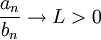 אזי הטורים a_n וb_n מתכנסים יחדיו (חברים). --ארז שיינר 20:41, 24 בינואר 2011 (IST)
אזי הטורים a_n וb_n מתכנסים יחדיו (חברים). --ארז שיינר 20:41, 24 בינואר 2011 (IST)
- וואו, לא היה זכור לי משפט כזה, מזל ששאלתי. תודה
- אני לא יודע אם זה בדיוק משפט. פשוט מבחן ההשוואה השני נובע מזה בקלות - קיים אפסילון כך ש
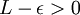 והחל משלב מסויים מתקיים
והחל משלב מסויים מתקיים 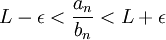 . --ארז שיינר 21:29, 24 בינואר 2011 (IST)
. --ארז שיינר 21:29, 24 בינואר 2011 (IST)
- אני לא יודע אם זה בדיוק משפט. פשוט מבחן ההשוואה השני נובע מזה בקלות - קיים אפסילון כך ש
- וואו, לא היה זכור לי משפט כזה, מזל ששאלתי. תודה
שאלה 1 מועד א 2007 של זלצמן
תהי 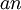 סדרה כך ש
סדרה כך ש 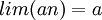 ו
ו 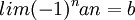 הוכח:
הוכח: 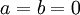
אשמח אם מישהו יגיד לי אם פתרתי נכון, כי אני לא כלכך בטוח בכך.
פתרון:
נניח ש 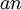 סדרה חיובית (בהמשך נוכיח לגבי סדרה שלילית וסדרה מעורבת או שאני אגיד שבאופן דומה אפשר להוכיח..)
סדרה חיובית (בהמשך נוכיח לגבי סדרה שלילית וסדרה מעורבת או שאני אגיד שבאופן דומה אפשר להוכיח..)
ידוע שהסדרה 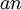 שואפת לגבול a ולכן נכתוב לפי הגדרת הגבול
שואפת לגבול a ולכן נכתוב לפי הגדרת הגבול
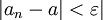
לכן גם
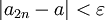 בנוסף,
בנוסף,
ניתן לתאר את הסדרה 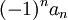 בצורה הבאה :
בצורה הבאה :
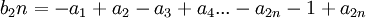 כלומר:
כלומר:
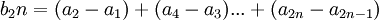
כלומר:
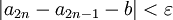 לפי הנתון.
לפי הנתון.
היות ו חיובית, נוכל לרשום(כמסקנה מהמשוואות עד עתה) את הדבר הבא
חיובית, נוכל לרשום(כמסקנה מהמשוואות עד עתה) את הדבר הבא
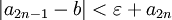
ולכן :
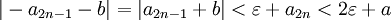
ולכן
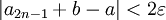
הגבול של  של
של 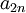 ושל
ושל 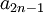 הוא אותו גבול
הוא אותו גבול
ולכן 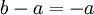
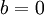
הצלחתי להגיע עד לפה. אשמח לדעת אם הפתרון שי עד לפה בסדר, ואם הוא טוב אז איך ממשיכים
פתרון נוסף
(לא מתרגל/ת): נראה לי שזה בסדר מה שעשית, אבל אני לא כל כך רואה איך אפשר להכליל את מה שעשית לסדרות אחרות, אשמח גם אני להסבר.
בכל אופן אני פתרתי את זה בדרך אחרת, אשמח למשוב:
הסדרה  היא מהצורה
היא מהצורה 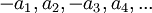 . ידוע שהיא מתכנסת לגבול
. ידוע שהיא מתכנסת לגבול 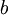 ולכן כל תת סדרה שלה תתכנס לגבול זה.
אם נתבונן בתת הסדרה של האיברים במקומות הזוגיים נקבל שהיא שואפת ל-
ולכן כל תת סדרה שלה תתכנס לגבול זה.
אם נתבונן בתת הסדרה של האיברים במקומות הזוגיים נקבל שהיא שואפת ל-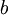 אבל באותו אופן גם ל-
אבל באותו אופן גם ל- (עפ"י נתון התכנסות הסדרה
(עפ"י נתון התכנסות הסדרה  ) ולכן
) ולכן 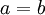 .
אם נתבונן בתת הסדרה של האיברים במקומות האי זוגיים נקבל שהיא שואפת ל-
.
אם נתבונן בתת הסדרה של האיברים במקומות האי זוגיים נקבל שהיא שואפת ל-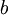 וגם ל
וגם ל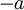 ולכן
ולכן 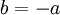 .
נפתור מערכת משוואות ונקבל ש-
.
נפתור מערכת משוואות ונקבל ש-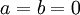 .
.
איך הפתרון הזה? תודה מראש, גל א.
(לא מתרגל/ת): הוספתי לאחר התנגשות עריכה - לא יודע לגבי ההוכחה הזו (אני יודע להוכיח את הטענות האלה, אבל ההוכחות לא מסתדרות עם ההסברים שלך. אולי התבלבת עם הפלוסים והמינוסים?), אבל ראה/י שאלה 7 בתרגיל 3.
התכנסות
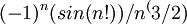 האם בגלל שהטור שואף ל0 זה מספיק כדי להגיד שתנאי לייבניץ מתקיים והוא מתכנס בתנאי?
האם בגלל שהטור שואף ל0 זה מספיק כדי להגיד שתנאי לייבניץ מתקיים והוא מתכנס בתנאי?
- (לא מתרגל/ת): לא. לשם כך תצטרך/י להראות גם ש-
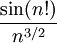 היא סדרה יורדת, מה שבוודאי אינו נכון. עם זאת, אפשר להראות שהטור מתכנס בהחלט:
היא סדרה יורדת, מה שבוודאי אינו נכון. עם זאת, אפשר להראות שהטור מתכנס בהחלט: 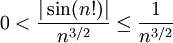 ובעזרת מבחן ההשוואה התכנסות הטור
ובעזרת מבחן ההשוואה התכנסות הטור 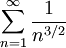 גוררת שהטור מתכנס.
גוררת שהטור מתכנס. 
כלל לופיטל
כאשר אני עושה את הנגזרת של המונה חלקי המכנה, מותר לי להתעסק עם השבר ולהעביר ביטויים מהמכנה למונה?
ואם נאי מעביר ביטויים מהמונה למכנה, כמו צמצום וכד' אז מותר לי להמשיך אחרי זה בגזירה?
- (לא מתרגל/ת): אחרי הגזירה - מותר, לפני - רק אם זה עדיין
 או
או  .
.
מבחן ההשוואה ה2
יוצא לי שאם ניקח לדוגמא: an = 1/n^2 ו bn = n אז נקבל שהחילוק בינהם הוא: an / bn = 1/n^3 והוא חסום בין 1 ל0. אזי אמורים להסיק שהטורים מתבדרים ביחד, מה שכמובן לא נכון.
אפשר קצת חידוד בנושא מבחן השוואה השני?
- לא יודע איך קיבלתם את מבחן ההשוואה בכיתה שלכם, אבל אצלנו (ד"ר הורוביץ) הוא ניתן כך:
אם 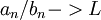 אז אם
אז אם  ∑ מתכנס אז
∑ מתכנס אז  ∑ מתכנס. אם
∑ מתכנס. אם 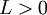 אז יתקיים שהטורים מתכנסים ומתבדרים יחד.
גרסה זו היא בהנתן טור חיובי.
מקווה שעזרתי! גל א.
אז יתקיים שהטורים מתכנסים ומתבדרים יחד.
גרסה זו היא בהנתן טור חיובי.
מקווה שעזרתי! גל א.
שאלה לגבי גבולות
מתי מותר לכתוב אם בכלל?
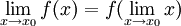
- (לא מתרגל/ת): כאשר f רציפה. שים/י לב שזה אותו דבר כמו
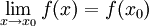 .
.
בשאלה ששואלים אותי  לא רציפה בהכרח ב
לא רציפה בהכרח ב 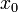
ומה קורה אם הפונקציה רציפה בכל הממשיים פרט ל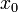
- (לא מתרגל/ת): אם היא לא רציפה ב-
 אז זה בהכרח לא נכון, כי אם
אז זה בהכרח לא נכון, כי אם 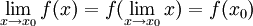 אז זה סותר את האי רציפות.
אז זה סותר את האי רציפות.
למה? הרי ש
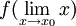 נותן את ערכי הפונקציה בסביבה של
נותן את ערכי הפונקציה בסביבה של 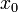 ולא את הערך ב
ולא את הערך ב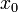 עצמו
עצמו
משפט רימן
לפי משפט רימן, שינוי סדרם של איבריו של טור מתכנס בתנאי יכול לשנות את המספר אליו מתכנס הטור או אפילו "לבדר" אותו. למרות זאת, כמה פעמים שינינו את סדרם של אינסוף איברים בטורים שאיננו יודעים אם הם מתכנסים (למשל פתרון שאלה 3 בתרגיל 7). מתי (אם בכלל) מותר לשנות את סדרם של אינסוף איברים בטור שלא ידוע שהוא מתכנס בהחלט?
עזרה בפתרון שאלה
אפשר עזרה בהוכחת הטענה הבאה?: אם a_n_(k+1)-a_n_k שואף לאפס כשK שואף לאינסוף לכל ת"ס של an, אז an סדרת קושי. אני לא מצליח להוכיח את הטענה ואפילו לא מבין למה בהכרח היא נכונה! תודה לעוזרים
איפה זה חדר מחלקה שבו יתקיים שיעור חזרה ביום חמישי הקרוב??
- (לא מתרגל/ת):
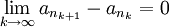 ולכן
ולכן 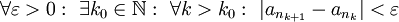 . זה נכון לכל תת סדרה של
. זה נכון לכל תת סדרה של 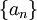 , כלומר לכל סדרה טבעית עולה ממש
, כלומר לכל סדרה טבעית עולה ממש 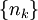 . לכן לכל m,n כך ש-m>n (בה"כ) נבחר סדרה
. לכן לכל m,n כך ש-m>n (בה"כ) נבחר סדרה 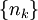 המקיימת
המקיימת 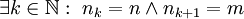 ולכן
ולכן 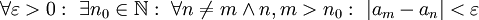 . אם m=n אז
. אם m=n אז 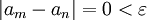 ולכן סדרת קושי.
ולכן סדרת קושי. 
- בקשר לחדר המחלקה, הוא נמצא בבניין 216 בחדר בקומה השנייה וכתוב על הדלת "חדר סטודנטים" (לא זוכר מה המספר).
- (לא אני שאלתי על החדר המחלקה, יש לשים את זה בכותרת נפרדת). אני לא בטוח שהפתרון הזה נכון, מכיוון שאני חושב שבפתרון הזה ה n0 תלוי ב-m ו-n, ואסור שתהיה תלות. תקנו אותי אם אני טועה?
הוכחת אינדוקציה
נשמח אם תוכל להסביר למה הסדרה (2 בחזקת n) לחלק ל(n בחזקת 2)תמיד גדולה או שווה לאחד? (באינדוקציה)
- (לא מתרגל)-נניח לn, אזי
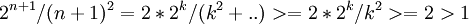 כשהשלב לפני אחרון לפני הנחת האינדוקציה.
כשהשלב לפני אחרון לפני הנחת האינדוקציה.