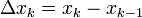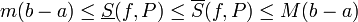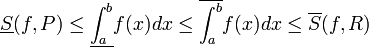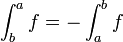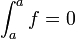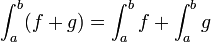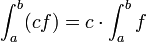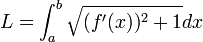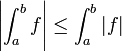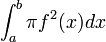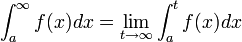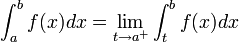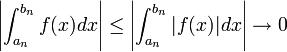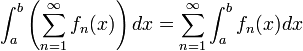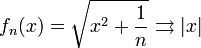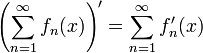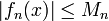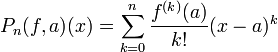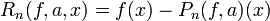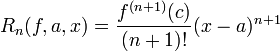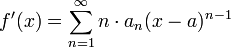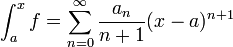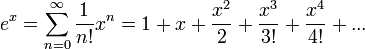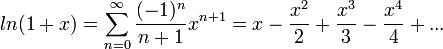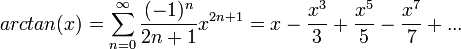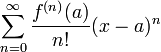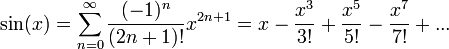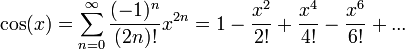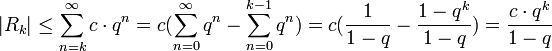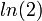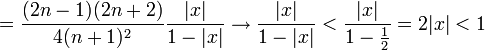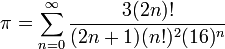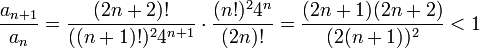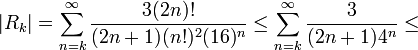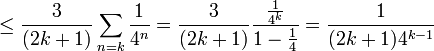חדוא 2 - ארז שיינר
אהבתם חדו"א 2? אז תעופו על חדו"א 1!
תוכן עניינים
- 1 מבחנים לדוגמא
- 2 סרטוני ותקציר ההרצאות
- 2.1 פרק 1 - האינטגרל הלא מסויים
- 2.2 פרק 2 - האינטגרל המסויים
- 2.3 פרק 3 - הקשר בין האינטגרל המסויים ללא מסויים
- 2.4 פרק 4 - אינטגרלים לא אמיתיים (מוכללים)
- 2.5 פרק 5 - סדרות וטורי פונקציות
- 2.6 פרק 6 - טורי טיילור וקירובים
מבחנים לדוגמא
מבחנים לדוגמא של מתמטיקה
- מועד א' החממה תשפ"א
- מועד ג' תשפ"א
- מועד ב' תשפ"א
- מועד א' תשפ"א, פתרון
- מועד ב' תש"ף
- מועד א' תש"ף, פתרון
- מועד ב' תשע"ט
- מועד א' תשע"ט, פתרון
- מועד ב' תשע"ח, פתרון חלקי
- מועד א' תשע"ח, פתרון
- מבחן דמה תשע"ז
- מועד ב' תשע"ז
- מועד א' תשע"ז, פתרון
- מבחן לדוגמא תשע"ה, פתרון חלקי
- מועד ג' תשע"ה, פתרון חלקי
- פתרון מועד ב' תשע"ה
- פתרון מועד א' תשע"ה
מבחנים לדוגמא של מדעי המחשב
שימו לב שפונקציות בשתי משתנים אינן בחומר שלנו.
מבחנים לדוגמא של מבוא לאנליזה 2 למורים
שימו לב שמדובר בקורס מבוא פחות מעמיק מהקורס שלנו.
מבחנים לדוגמא של חדו"א 1 להנדסה
שימו לב שאלות 2 ו6 תמיד רלוונטיות לקורס זה.
סרטוני ותקציר ההרצאות
פרק 1 - האינטגרל הלא מסויים
- הגדרה: F נקראת פונקציה קדומה של f בקטע A אם לכל נקודה בקטע מתקיים כי
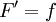
- האינטגרל הלא מסויים
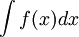 מסמן פונקציה קדומה של f.
מסמן פונקציה קדומה של f.
- תהי F קדומה של f, אזי קבוצת כל הקדומות של f שווה ל
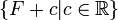
- אינטגרלים מיידיים ידועים לנו מנוסחאות הגזירה.
שיטות למציאת קדומה
- תהיינה f,g פונקציות בעלות קדומות, אזי:
אינטגרציה בחלקים
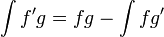
שיטת הההצבה
פונקציה רציונאלית
- פולינום הוא פונקציה מהצורה
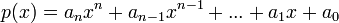
- דרגת הפולינום היא n אם
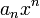 הוא המונום עם החזקה הגבוהה ביותר כך ש
הוא המונום עם החזקה הגבוהה ביותר כך ש 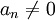
- אפשר לומר שדרגת פולינום האפס היא מינוס אינסוף.
- פולינום נקרא פריק אם ניתן להציג אותו כמכפלה של פולינומים מדרגה 1 ומעלה, נעסוק בפולינומים ממשיים בלבד בהקשר זה.
- פולינום מדרגה 1 אינו פריק
- פולינום מדרגה 2 (פרבולה) פריק אם ורק אם יש לו שורש ממשי.
- כל פולינום מדרגה 3 ומעלה פריק.
- מציאת שורשים של פולינום ופירוקו -
- ננחש שורש ונבדוק שהוא אכן מאפס את הפולינום ע"י הצבה
- אם a שורש, נחלק את הפולינום ב
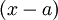
- כך הלאה.
- הורדת דרגת המונה ע"י חילוק פולינומים
- שבר חלקי של גורם אי פריק לינארי
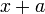 הוא ביטוי מהצורה
הוא ביטוי מהצורה 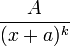
- שבר חלקי של גורם אי פריק ריבועי
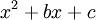 (כך שאין לו שורשים ממשיים) הוא ביטוי מהצורה
(כך שאין לו שורשים ממשיים) הוא ביטוי מהצורה 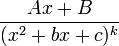
- כל פונקציה רציונאלית בה דרגת המונה קטנה ממש מדרגת המכנה ניתן להציג באופן יחיד כסכום של שברים חלקיים (כפול קבוע).
- פירוק לשברים חלקיים
- חישוב אינטגרל של כל שבר חלקי
- נסמן
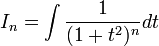
- אזי
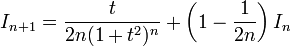
- נסמן
כאשר תנאי ההתחלה הוא 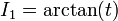
הצבות אוניברסאליות
הצבות אוניברסאליות הוא כינוי כללי להצבות המעבירות פונקציות ממשפחה מסוימת לצורה של פונקציה רציונאלית אותה אנחנו יודעים לפתור. שימו לב שכיון ופתרון פונקציה רציונאלית דורש פירוק פולינומים, לעתים המעבר לפונקציה רציונאלית לא יקדם אותנו לקראת פתרון הבעיה.
פרק 2 - האינטגרל המסויים
סכומי דרבו ואינטגרל עליון ותחתון
הגדרת סכומי דרבו, אינטגרביליות והאינטגרל המסוים
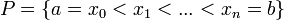 היא חלוקה של הקטע
היא חלוקה של הקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
- תהי f חסומה בקטע, ותהי P חלוקה של הקטע.
- נסמן
- נגדיר
- סכום דרבו עליון
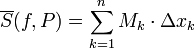
- סכום דרבו תחתון
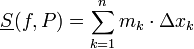
- סכום דרבו עליון
- תהי f פונקציה חסומה בקטע.
- נסמן את קבוצת כל סכומי הדרבו העליונים על כל החלוקות של הקטע ב
- נסמן את קבוצת כל סכומי הדרבו התחתונים על כל החלוקות של הקטע ב
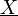
- נגדיר את האינטגרל העליון להיות
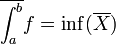
- נגדיר את האינטגרל התחתון להיות
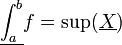
- נגדיר שf אינטגרבילית בקטע אם
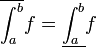
- במקרה שf אינטגרבילית נגדיר את האינטגרל המסויים שלה להיות
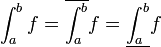
- דוגמא:
- פונקצית דיריכלה היא
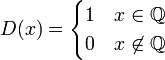
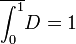
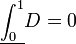
- לכן פונקצית דיריכלה אינה אינטגרבילית בקטע
![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.
תכונות של סכומי דרבו והאינטגרל המסוים
- נגדיר את פרמטר של חלוקה להיות אורך תת הקטע הגדול ביותר:
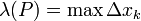
- תהי חלוקה
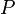 ותהי העדנה שלה
ותהי העדנה שלה 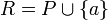
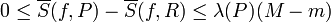
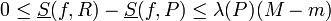
התכנסות סכומי דרבו
- התכנסות סכומי הדרבו העליונים לאינטגרל העליון
- תהי f פונקציה חסומה בקטע.
- תהי סדרת חלוקות של הקטע
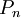 כך ש
כך ש 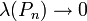
- אזי
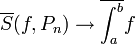
- כמובן שבאופן דומה
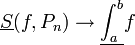
פונקציות אינטגרביליות
- פונקציה רציפה בקטע סגור אינטגרבילית בו
- תהי f אינטגרבילית בקטעים
![[a,b],[b,c]](/images/math/c/5/2/c52dbf748279117b1d8a4edf372c0270.png) אזי:
אזי:
- היא אינטגרבילית בקטע
![[a,c]](/images/math/2/0/9/209f61583177d88b1f24c85f6a43c6ff.png)
- מתקיים כי
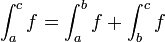
- היא אינטגרבילית בקטע
- פונקציה חסומה בקטע סופי, ורציפה פרט למספר סופי של נקודות, אינטגרבילית בו
- לכל פונקציה אינטגרבילית בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) נגדיר כי:
נגדיר כי:
- תרגיל: אם
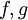 אינטגרביליות ב
אינטגרביליות ב![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) אזי
אזי 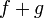 אינטגרבילית בקטע, וכך גם
אינטגרבילית בקטע, וכך גם 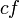 לכל קבוע
לכל קבוע 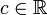 . כמו כן מתקיים כי:
. כמו כן מתקיים כי:
סכומי רימן
- תהי f המוגדרת בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
- תהי P חלוקה של הקטע
- תהי
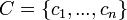 קבוצת נקודות בתתי הקטעים
קבוצת נקודות בתתי הקטעים ![c_k\in[x_{k-1},x_k]](/images/math/c/b/b/cbbb2a7a61cd7e98c21895f0cabd6417.png)
- נגדיר את סכום הרימן
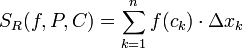
- אומרים שf אינטגרבילית רימן בקטע אם קיים גודל סופי
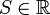 כך ש:
כך ש:
- לכל סדרת חלוקות
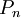 המקיימת
המקיימת 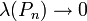
- ולכל סדרת בחירת נקודות
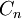 המתאימה לחלוקות
המתאימה לחלוקות - מתקיים כי
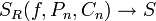
- לכל סדרת חלוקות
- במקרה שf אינטגרבילית רימן בקטע מסמנים
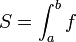
- משפט: f אינטגרבילית רימן בקטע אם"ם f חסומה בקטע ואינטגרבילית (לפי דרבו)
- כמו כן, במקרה שהפונקציה אינטגרבילית, האינטגרל המסויים שווה לפי רימן ולפי דרבו.
- משפט מאד שימושי:
- תהי פונקציה
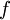 הרציפה בקטע הסגור
הרציפה בקטע הסגור ![[0,1]](/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) אזי:
אזי: 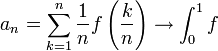
- תהי פונקציה
אורך עקומה
אי שיוויון המשולש לאינטגרלים
פרק 3 - הקשר בין האינטגרל המסויים ללא מסויים
כבר במאות ה4 וה3 לפנה"ס אוקלידס וארכימדס ידעו לחשב היקפים, שטחים ונפחים, אך רק במאה ה17 לספירה ניוטון ולייבניץ המציאו את החשבון הדיפרנציאלי והאינטגרלי.
כלומר, ההבנה שיש קשר בין שטחים (האינטגרל המסויים) לבין פונקציות קדומות (אינטגרל לא מסוים) הגיעה כמעט 2000 שנה לאחר שכבר ידעו לחשב שטחים.
בפרק זה נוכיח את הקשר הזה שבין החשבון הדיפרנציאלי לאינטגרלי בעזרת המשפט היסודי של החדו"א.
המשפט היסודי של החדו"א
- עבור פונקציה אינטגרבילית, בנקודות בהן היא רציפה מתקיים כי
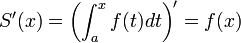
נוסחאת ניוטון לייבניץ
- תהי f אינטגרבילית וF קדומה אזי
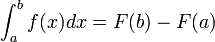
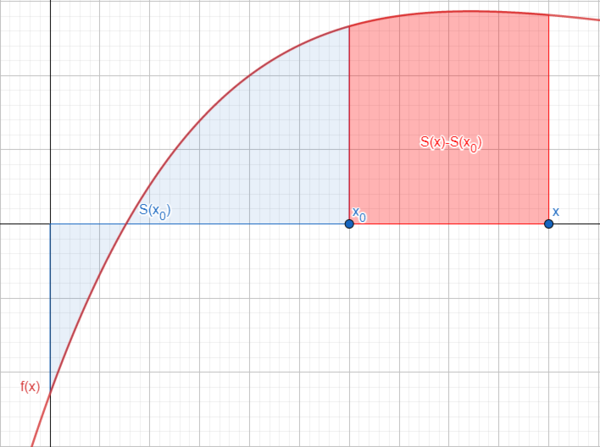
גרסא חלשה ופשוטה של המשפט היסודי
- תהי
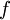 פונקציה רציפה בקטע
פונקציה רציפה בקטע ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ותהי
ותהי 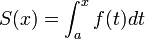 פונקצית השטח שלה.
פונקצית השטח שלה. - אזי לכל
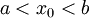 מתקיים כי
מתקיים כי 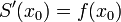
הוכחה
- לפי משפט ערך הממוצע האינטגרלי לכל x בקטע קיימת c בקטע כך ש
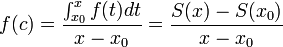
- לכן לכל סדרה
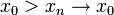 קיימת סדרת נקודות
קיימת סדרת נקודות 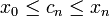 כך ש
כך ש 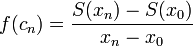
- לפי משפט הסנדביץ'
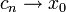 וכיוון ש
וכיוון ש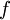 רציפה, נובע כי
רציפה, נובע כי 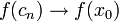
- לכן קיבלנו כי
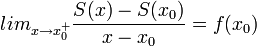
- ניתן להוכיח באופן דומה שזה גם הגבול השמאלי, ובסה"כ לפי הגדרת הנגזרת קיבלנו כי
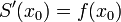
הגדרת המספר π, וחישוב היקף ושטח מעגל
נפח גוף סיבוב
פרק 4 - אינטגרלים לא אמיתיים (מוכללים)
השופר של גבריאל
הגדרת אינטגרלים לא אמיתיים
- תהי f אינטגרבילית בקטע
![[a,t]](/images/math/4/1/d/41db424f5c02cc7c51f1f480735df0e4.png) לכל
לכל 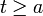 אזי:
אזי:
- תהי f שאינה חסומה בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ואינטגרבילית בקטע
ואינטגרבילית בקטע ![[t,b]](/images/math/6/6/c/66ce2d41698b246a23f9e4be3153c8cf.png) לכל
לכל 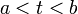 אזי:
אזי:
- משפט:
- האינטגרל
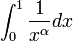 מתכנס אם ורק אם
מתכנס אם ורק אם 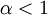
- האינטגרל
 מתכנס אם ורק אם
מתכנס אם ורק אם 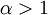
- האינטגרל
- הערה: נניח
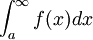 מתכנס, האם
מתכנס, האם 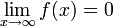 ?
?
- בלי נתונים נוספים
- כאשר f רציפה
- כאשר f רציפה וחיובית
- כאשר נתון שלf יש גבול
מבחני השוואה לאינטגרלים חיוביים
- מבחן ההשוואה הראשון:
- תהיינה
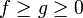 עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית אזי-
עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית אזי- - אם
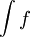 מתכנס בקטע, גם
מתכנס בקטע, גם 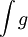 מתכנס בקטע
מתכנס בקטע
- תהיינה
- מבחן ההשוואה הגבולי:
- תהיינה
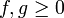 עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית.
עבורן מוגדר אינטגרל לא אמיתי באותו הקטע עם אותה הנקודה הבעייתית. - נחשב בנוסף את הגבול בנקודה הבעייתית
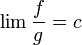 .
. - אזי:
- אם
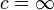 , אזי אם
, אזי אם 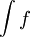 מתכנס גם
מתכנס גם 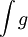 מתכנס.
מתכנס. - אם
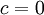 אזי אם
אזי אם 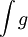 מתכנס גם
מתכנס גם 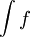 מתכנס.
מתכנס. - אם
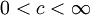 אזי האינטגרלים חברים
אזי האינטגרלים חברים 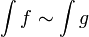 כלומר שניהם מתכנסים או שניהם מתבדרים.
כלומר שניהם מתכנסים או שניהם מתבדרים.
- אם
- תהיינה
התכנסות בהחלט וקריטריון היינה
- קריטריון היינה:
- אינטגרל לא אמיתי מקיים קריטריון היינה אם לכל שתי סדרות בקטע השואפות לנקודה הבעייתית מתקיים כי:
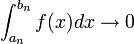
- אינטגרל לא אמיתי מתכנס אם"ם הוא מקיים את קריטריון היינה.
- פונקציה
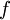 עליה מוגדר אינטגרל לא אמיתי נקראת מתכנסת בהחלט בקטע אם
עליה מוגדר אינטגרל לא אמיתי נקראת מתכנסת בהחלט בקטע אם 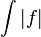 מתכנס בקטע.
מתכנס בקטע.
- פונקציה מתכנסת בהחלט בקטע מתכנסת.
מבחן דיריכלה
- תהי פונקציה
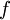 אשר מקיימת 3 תנאים בקטע
אשר מקיימת 3 תנאים בקטע 
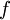 מונוטונית יורדת
מונוטונית יורדת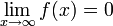
- הנגזרת
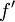 רציפה.
רציפה.
- תהי בנוסף פונקציה
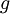 אשר מקיימת 2 תנאים באותו הקטע:
אשר מקיימת 2 תנאים באותו הקטע:
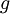 רציפה.
רציפה.- ל
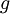 יש קדומה
יש קדומה 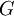 חסומה.
חסומה.
- אזי האינטגרל
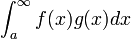 מתכנס.
מתכנס.
פרק 5 - סדרות וטורי פונקציות
פונקצית הגבול
העשרה - סוגי סכימה שונים
התכנסות במ"ש
- בדיקת התכנסות במ"ש:
- נחשב את פונקצית הגבול. בשלב זה x קבוע וn שואף לאינסוף.
- נחשב את סדרת החסמים
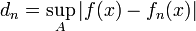 . בשלב זה n קבוע, וx נע בקטע A.
. בשלב זה n קבוע, וx נע בקטע A. - יש התכנסות במ"ש אם"ם
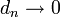 .
.
- אם סדרה מתכנסת במ"ש בקטע, וכל הפונקציות בסדרה רציפות בנק' מסויימת, גם פונקצית הגבול רציפה באותה נקודה.
אינטגרציה וגזירה איבר איבר
- סדרת פונקציות אינטגרביליות המתכנסת במ"ש, מתכנסת לפונקציה אינטגרבילית.
- כמו כן, במקרה זה, סדרת שטחי הפונקציות מתכנסת לשטח פונקצית הגבול.
- עבור טור פונקציות אינטגרביליות המתכנס במ"ש מתקיים כי:
- דוגמא: סדרת פונקציות גזירות המתכנסת במ"ש לפונקצית גבול שאינה גזירה
- סדרת פונקציות המתכנסת בנקודה, שנגזרותיה רציפות ומתכנסות במ"ש בA מקיימת בA:
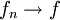 וגם
וגם 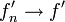
- טור פונקציות המתכנס בנקודה, שנגזרותיו רציפות וטור הנגזרות מתכנס במ"ש בA מקיים בA:
מבחן הM של ויירשטראס
- תהי סדרת פונקציות החסומה בערך מוחלט ע"י סדרת מספרים בקטע A:
- אזי אם טור המספרים
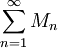 מתכנס, טור הפונקציות
מתכנס, טור הפונקציות 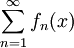 מתכנס במ"ש בקטע A.
מתכנס במ"ש בקטע A.
פרק 6 - טורי טיילור וקירובים
פולינום טיילור
- הקדמה
- פולינום טיילור
- שארית טיילור
- שארית טיילור בצורת לגראנז'
- תהי f הגזירה n+1 פעמים בסביבה של a ותהי נקודה בסביבה זו. אזי קיימת נקודה c בין a לx כך שהשארית מקיימת:
- הוכחת שארית טיילור בצורת לגראנז'
- נפעיל את משפט קושי על הפונקציות
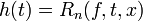 ו
ו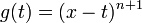 בקטע שבין a ל x.
בקטע שבין a ל x.
- נפעיל את משפט קושי על הפונקציות
- שארית פיאנו
- תהי
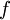 הגזירה
הגזירה  פעמים בסביבה של
פעמים בסביבה של 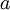 . אזי:
. אזי:
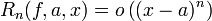
- כלומר
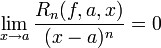
טורי חזקות/טיילור/מקלורן
- הגדרת טורי חזקות
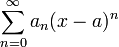
רדיוס התכנסות
- הגדרת רדיוס התכנסות
![R=\frac{1}{\overline{\lim} \sqrt[n]{|a_n|}}](/images/math/b/f/b/bfb609528022a36fcabe61f5bd10c387.png)
- אם הגבול של המנה קיים במובן הרחב, אזי
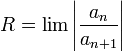
- רדיוס ההתכנסות אומר לנו על תחום ההתכנסות:
- אם
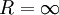 אזי הטור מתכנס בהחלט בכל הממשיים.
אזי הטור מתכנס בהחלט בכל הממשיים. - אם
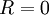 הטור מתכנס רק עבור
הטור מתכנס רק עבור 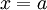 .
. - אם
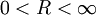 אזי
אזי
- הטור מתכנס בהחלט בתחום
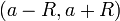 .
. - הטור מתבדר כאשר
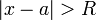 .
. - את שני הקצוות
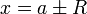 צריך להציב, ולבחון את התכנסות טורי המספרים שנקבל באמצעות מבחני התכנסות.
צריך להציב, ולבחון את התכנסות טורי המספרים שנקבל באמצעות מבחני התכנסות.
- הטור מתכנס בהחלט בתחום
- כאשר
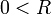 אזי לכל
אזי לכל 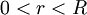 מתקיים כי הטור מתכנס במ"ש בתחום
מתקיים כי הטור מתכנס במ"ש בתחום ![[a-r,a+r]](/images/math/1/d/8/1d815134a9d14aeb1828a51ebe06bedb.png)
- אם
- דוגמא לחישוב תחומי ההתכנסות של טורי החזקות
- עבור טור חזקות מהצורה
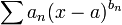 מתקיים כי רדיוס ההתכנסות הינו
מתקיים כי רדיוס ההתכנסות הינו ![R=\frac{1}{\overline{\lim} \sqrt[b_n]{|a_n|}}](/images/math/e/f/2/ef222e55405e5159be01a4dd0e20b825.png)
פיתוח טורי טיילור
- גזירה ואינטגרציה איבר איבר של טורי חזקות
- יהי טור חזקות בעל רדיוס התכנסות
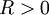
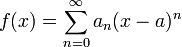
- אזי לכל x המקיים
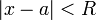 מתקיים כי:
מתקיים כי:
- פיתוח טורי טיילור באמצעות גזירה ואינטגרציה
יחידות וקיום טור טיילור
- עבור פונקציה הגזירה אינסוף פעמים בסביבת הנקודה a טור הטיילור הוא:
- אם פונקציה שווה לטור חזקות בעל רדיוס התכנסות חיובי בקטע, אזי זה טור הטיילור שלה.
- ייתכן שפונקציה גזירה אינסוף פעמיים בכל הממשיים, טור הטיילור שלה בעל רדיוס התכנסות חיובי, ועדיין אינו מתכנס אליה פרט לנקודה סביבה פיתחנו.
- דוגמא:
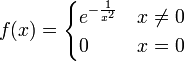
- מתקיים כי
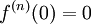 לכל n.
לכל n. - לכן טור הטיילור של הפונקציה הוא טור אפסים, אבל הפונקציה אינה שווה לאפס פרט לנקודה
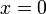 .
.
טורי הטיילור של סינוס וקוסינוס, ואקספוננט של מספר מרוכב
- נוכיח כי
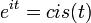
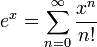
- נגדיר את e בחזקת מרוכב באמצעות טור הטיילור, ונציב:
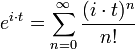
- נפריד לסכום האיברים במקומות הזוגיים והאי זוגיים.
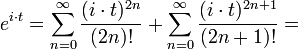
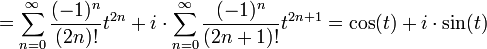
- זה מוביל לזהות אוילר המפורסמת
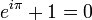
משפט אבל על התכנסות בקצה התחום
- יהי טור
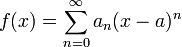 עם רדיוס התכנסות
עם רדיוס התכנסות 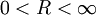 .
. - אם
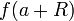 מתכנס אזי
מתכנס אזי 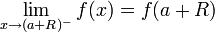
- אם
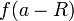 מתכנס אזי
מתכנס אזי 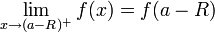
קירובים והערכות שגיאה
שיטות הערכות שגיאה - לגראנז', לייבניץ, חסימה על ידי טור הנדסי
- יהי טור
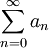
- קירוב מסדר k לטור הוא
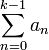 , זהו סכום k האיברים הראשונים.
, זהו סכום k האיברים הראשונים. - השגיאה עבור קירוב זה היא כמובן
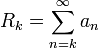
- קירוב מסדר k לטור הוא
- אם מדובר בטור לייבניץ, השגיאה מקיימת
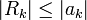 לפי מבחן לייבניץ להתכנסות טורים.
לפי מבחן לייבניץ להתכנסות טורים.
- אם הטור חסום ע"י טור הנדסי אזי השגיאה מקיימת:
- בסרטון נקרב את המספרים הבאים:
טור הטיילור של ההופכית של סינוס, וקירוב מהיר של π
- נביט בפונקציה
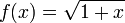
- נוכיח באינדוקציה כי הנגזרת מסדר n הינה:
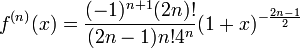
- עבור n=1 אכן מתקיים כי
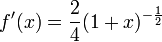
- יהי n עבורו הטענה נכונה, צ"ל כי
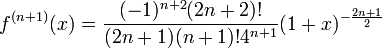
- צ"ל
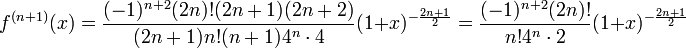
- אכן בעזרת הנחת האינדוקציה
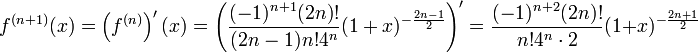
- עבור n=1 אכן מתקיים כי
- לכן טור המקלורן של
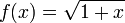 הינו
הינו 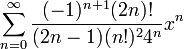
- על מנת להוכיח שהוא שווה לפונקציה, צ"ל שהשגיאה שואפת לאפס.
- יהי
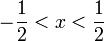 , נוכיח שהשגיאה עבורו שואפת לאפס.
, נוכיח שהשגיאה עבורו שואפת לאפס. 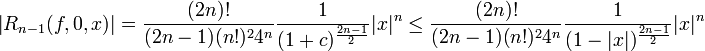
- נחשב את גבול המנה של הביטוי שקיבלנו:
- לכן לפי מבחן המנה השגיאה שואפת לאפס בתחום זה, וטור המקלורן מתכנס לפונקציה בתחום זה.
- הוכחנו שבתחום
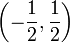 מתקיים
מתקיים 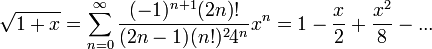
- נגזור ונקבל שבקטע מתקיים
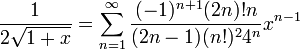
- נבצע הזזת אינדקסים
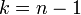 ונקבל
ונקבל 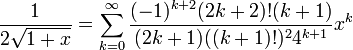
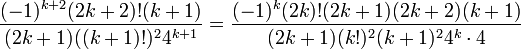
- סה"כ בתחום זה נקבל
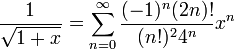
- נציב
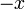 ונקבל באותו תחום
ונקבל באותו תחום 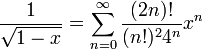
- הערה - טורי הטיילור שפיתחנו כאן מתכנסים בעצם לפונקציות שלהן בתחום בין מינוס אחד לאחד, אך ההוכחה של זה מורכבת יותר ולא נחוצה לנו כרגע.
- כעת נציב
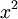 ונקבל שבתחום
ונקבל שבתחום 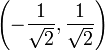 מתקיים
מתקיים 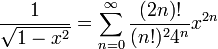
- נבצע אינטגרציה מ0 עד x ונקבל
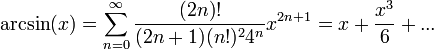
- נציב
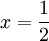 שנמצא בתחום ונקבל:
שנמצא בתחום ונקבל: 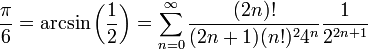
- ולכן
- כעת המנה של הסדרה
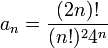 היא
היא
- לכן מדובר בסדרה יורדת שכל איבריה קטנים או שווים ל
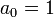
- לכן
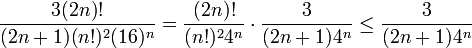
- לכן בקירוב
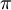 ע"י k האיברים הראשונים נקבל שגיאה:
ע"י k האיברים הראשונים נקבל שגיאה:
- למשל, קירוב של 6 האיברים הראשונים יספק שגיאה קטנה מ
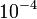 כלומר רמת דיוק של 4 ספרות אחרי הנקודה העשרונית, לפחות.
כלומר רמת דיוק של 4 ספרות אחרי הנקודה העשרונית, לפחות. 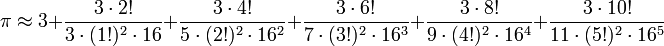
אהבתם חדו"א 2? אז תעופו על חדו"א 1!
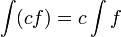
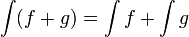
![\displaystyle{M_k=\sup_{[x_{k-1},x_k]}(f)}](/images/math/c/9/1/c913686ddc3ca56d222438af9f75503a.png)
![\displaystyle{m_k=\inf_{[x_{k-1},x_k]}(f)}](/images/math/0/e/2/0e20a2d835750acfec3c81ca47fd447e.png)