מרצה: פרופ' בועז צבאן.
מתרגלת: תמר בר-און.
דרישות הקורס: תרגיל (20% מהציון הסופי), מטלות קריאה עצמית, מבחן (80% מהציון הסופי). חובה להגיש לפחות 70% מתרגילי הבית (מעוגל כלפי מעלה) כדי לקבל ציון בקורס.
הודעות
דברים שלא יופיעו במבחן: כמו שהסברתי בהרצאה האחרונה, הנושא ״מערכות של מספרים״ (הכולל את בניית השלמים, הרציונלים והממשיים, חתכי דדקינד ומשפט החסם העליון) לא יופיע במבחן. כמו כן, משפט גודשטיין לא יופיע כנושא שצריך להכיר מראש (אם כי איני שולל שמשהו דומה או חלקי יופיע כתרגיל, כאשר ההגדרות הנחוצות יסופקו במבחן). מטלות הקריאה המודרכת הם חלק מהחומר למבחן. כהקלה נוספת, בכל מועד תופיע לפחות שאלה אחת מהתרגיל: מתרגיל בית, משיעור התרגיל, או וריאציה של שאלה כזו.
סקר שביעות הרצון מההוראה בקורס: כדי שיהיה משוב על הקורס, חשוב שכל תלמיד שנכח בהרצאות, אפילו בחלקן, ימלא את סקר ההוראה של הקורס. השתתפותכם בסקר רצויה ומוערכת.
מבחנים של פרופ' צבאן משנים קודמות אפשר למצוא כאן. אין הרבה מבחנים. כדאי להסתכל גם במבחנים של פרופ' רינות (ייתכנו שם נושאים שאינם בקורס שלנו, ולהיפך, אך ההבדל אינו גדול).
מטלת קריאה שלישית בקורס: הוכחת המשפט שהמרחב הוא איחוד מעגלים זרים.
מטלת קריאה שניה בקורס: הוכחת הטענה האחרונה מההרצאה בנושא האלפים, ועוד תכונה של אלפים.
מטלת קריאה ראשונה בקורס: הוכחת משפט הרקורסיה (+דוגמא מפורטת כבונוס).
רשימת הנושאים שכיסינו בתרגול
קבוצות סדורות. סדר צפוף. סדר טוב.
תת קבוצות קופינליות.
פונקציות שומרות סדר, איזומורפיזם סדר.
סודרים (הגדרה ותכונות).
סודרים עוקבים וגבוליים.
ארתמטיקה של סודרים: חיבור, חיסור, כפל, חילוק עם שארית, חזקות, הצגה לפי בסיס.
פונקציות מונוטוניות ורציפות.
טופולוגיית הסדר.
אקסיומות zf.
אקסיומת הבחירה ושיקולים: עקרון הסדר הטוב, הלמה של צורן.
עוצמות וסודרים מונים.
ארתמטיקה של עוצמות.
קופינליות של סודרים.
בוחן
בוחן בקורס יתקיים ביום ראשון, 16.12, בשעה 14:00-15:30 (בזמן התרגול).
חומר לבוחן: כל מה שנלמד עד תרגול 7, כולל. בפירוט:
קבוצות סדורות. סדר צפוף. סדר טוב.
תת קבוצות קופינליות.
פונקציות שומרות סדר, איזומורפיזם סדר.
סודרים (הגדרה ותכונות).
סודרים עוקבים וגבוליים.
ארתמטיקה של סודרים: חיבור, חיסור, כפל, חילוק עם שארית, חזקות, הצגה לפי בסיס.
פונקציות מונוטוניות ורציפות.
טופולוגיית הסדר.
בבוחן יכולות להופיע שאלות מהתרגול/ מש"ב, כמו גם שאלות חדשות.
תקציר הקורס
תקציר הקורס המתעדכן. מתעדכן מדי הרצאה, ולכן לא מומלץ להורידו אלא לקרוא תמיד מהקישור.
בעיית המידה של לבג. סיכום בסגנון קצת שונה מאיך שהצגנו בהרצאה, אבל ההרצאה הלכה לפיו, והמתמטיקה זהה. כולל פרק בונוס, "עוד על מונים מדידים".
תרגילים
הערה: בשאלה 3 א' יש לדרוש: 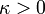 .
.
תרגיל 12 תרגיל רשות
יש להגיש את כל התרגילים החסרים עד 19.01, על מנת שאוכל להעלות לכם פתרונות לפני המבחן.
העשרה
איך לספור מעבר לאינסוף: סרטון המסביר באופן מאד ויזואלי ויפה, את המושגים המרכזיים בחלק הראשון של הקורס.
משפט גודשטיין: הערך בויקיפדיה. מכיל דוגמאות מפורטות של סדרות, והרחבות שונות.
הפרדוקס של בנך-טרסקי: איך אפשר - תיאורטית - להפוך כדור זהב אחד לשניים, בעזרת אקסיומת הבחירה.