סמסטר	שם הקורס	מספר ההרצאה	מרצה	מספר התרגול	מתרגל/ת
קיץ תש"ע	מתמטיקה בדידה	88-195-11	ד"ר שי סרוסי	88-112-12	גב' שני תורג'מן
קיץ תש"ע	אלגברה לינארית 1	88-112-08	ד"ר אלי בגנו	88-112-09	גב' רונית כץ
א תשע"א	אלגברה לינארית 2	88-113-08	ד"ר בועז צבאן	88-113-09	מר דורון פרלמן
א תשע"א	חשבון אינפיניטסימלי 1	88-132-07	ד"ר שמחה הורוביץ'	88-132-08	ד"ר אפי כהן
קורסים נוכחיים
ב תשע"א	חשבון אינפיניטסימלי 2	88-133-07	ד"ר שמחה הורוביץ'	88-113-08	מר שי גול
ב תשע"א	שימושי מחשב במתמטיקה	88-151-06	פרופ' ג'רמי שיף	88-151-08	מר גרגורי אושרוביץ

סטודנט לתואר ראשון (שנה ראשונה) במתמטיקה ותלמיד תיכון.

תוכן עניינים

1 תקצירי קורסים
- 1.1 אינפי 2
  - 1.1.1 הרצאות
  - 1.1.2 תרגולים
2 בגלל התקלה באתר, באופן זמני אני כותב את הרצאה 4 פה, 1.3
- 2.1 משפט 12 (המשפט היסודי של חשבון אינטגרלי)
  - 2.1.1 הוכחה
- 2.2 מסקנה

תקצירי קורסים

בהרצאות ובתרגולים הראשונים של אינפי 2 ניסיתי לסכם את הקורס במחשב במקום במחברת. בהמשך אני אחליט אם לחזור למחברת או להשאר במחשב, אבל בינתיים כל אחד יכול להסתכל עליהם, לערוך אותם, לתקן שגיאות (מכל סוג) וכו'.

אינפי 2

הרצאות

(את ההרצאה ה-3 לא יכולתי לתקן בגלל התקלה באתר. יטופל בהמשך)

תרגולים

(כנ"ל לגבי התרגול ה-2)

בגלל התקלה באתר, באופן זמני אני כותב את הרצאה 4 פה, 1.3

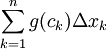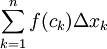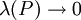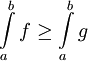המשך ההוכחות לשמפט 11: ב - נתבונן בסכום רימן כלשהו עבור g: $\sum_{k=1}^n g(c_k)\Delta x_k$ . לפי הנתון הוא קטן או שווה ל- $\sum_{k=1}^n f(c_k)\Delta x_k$ . נשאיף $\lambda(P)\to0$ . סכומים אלה שואפים לאינטגרלים של f ו-g ונסיק $\int\limits_a^b f\ge\int\limits_a^b g$ . $\blacksquare$

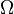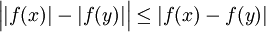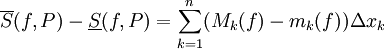ג - נעיר ש- $\Omega$ היא בעצם $\Omega(f)=\sup\{|f(x)-f(y)|:\ x,y\in[a,b]\}$ . כזכור, אי שיוויון המשולש אומר ש- $\Big||f(x)|-|f(y)|\Big|\le|f(x)-f(y)|$ . נובע ש- $\Omega(|f|)=\sup\{\Big||f(x)|-|f(y)|\Big|:\ x,y\in[a,b]\}\le\sup\{|f(x)-f(y)|:\ x,y\in[a,b]\}=\Omega(f)$ . כעת תהי P חלוקה כלשהי של $[a,b]$ $\overline S(f,P)-\underline S(f,P)=\sum_{k=1}^n (M_k(f)-m_k(f))\Delta x_k$ . נעיר שלכל 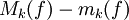$M_k(f)-m_k(f)$ היא התנודה של f בקטע $[x_{k-1},x_k]$ ולפי מה שהוכחנו זה גדול או שווה לתנודה של |f| באותו קטע.

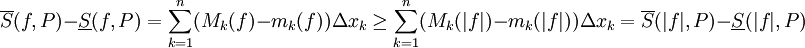$\overline S(f,P)-\underline S(f,P)=\sum_{k=1}^n (M_k(f)-m_k(f))\Delta x_k\ge\sum_{k=1}^n (M_k(|f|)-m_k(|f|))\Delta x_k=\overline S(|f|,P)-\underline S(|f|,P)$ . כעת נוכיח ש-|f| אינטגרבילית. לצורך זה יהי 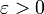$\varepsilon>0$ נתון. כיוון ש-f אינטגרבילית (נתון) קיימת חלוקה P של [a,b] כך ש- 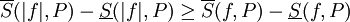$\overline S(|f|,P)-\underline S(|f|,P)\ge\overline S(f,P)-\underline S(f,P)$ ונובע ממשפט 5 ש-|f| אינטגרבילית. לגבי אי השיוויון נעיר שלכל סכום רימן ל-f

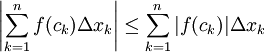$\left|\sum_{k=1}^n f(c_k)\Delta x_k\right|\le\sum_{k=1}^n |f(c_k)|\Delta x_k$ . נשאיף 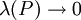$\lambda(P)\to0$ להסיק ש-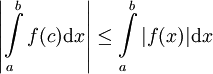 $\left|\int\limits_a^b f(c)\mathrm dx\right|\le\int\limits_a^b|f(x)|\mathrm dx$

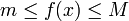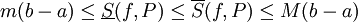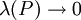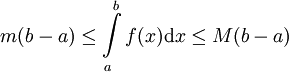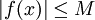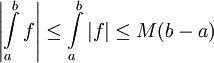ד - נתון $m\le f(x)\le M$ . לפי משפט 1, לכל חלוקה P של $[a,b]$ מתקיים $m(b-a)\le\underline S(f,P)\le\overline S(f,P)\le M(b-a)$ . נשאיף את $\lambda(P)\to0$ להסיק $m(b-a)\le\int\limits_a^b f(x)\mathrm dx\le M(b-a)$ ואם נתון $|f(x)|\le M$ אז נוכל להסתמך על סעיף ג ומה שהוכחנו הרגע לומר $\left|\int\limits_a^b f\right|\le\int\limits_a^b |f|\le M(b-a)$ .

ה - לפי הנתון 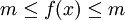$m\le f(x)\le m$ . לכן, עפ"י סעיף ד 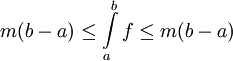$m(b-a)\le\int\limits_a^b f\le m(b-a)$ ויש שיוויון. $\blacksquare$

משפט 12 (המשפט היסודי של חשבון אינטגרלי)

תהי f מוגדרת ואינטגרבילית בקטע $[a,b]$

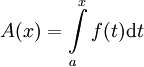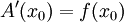לכל $x\in[a,b]$ נגדיר $A(x)=\int\limits_a^x f(t)\mathrm dt$ . אזי A מוגדרת היטב ורציפה ב- $[a,b]$ ולכל $x_0\in[a,b]$ שבה f רציפה A גזירה כך ש- $A'(x_0)=f(x_0)$ .
(נוסחת ניוטון-לייבניץ): נניח ש-f רציפה בכל הקטע $[a,b]$ . אם F קדומה ל-f אז $\int\limits_a^b f=[F(x)]_{x=a}^b=F(b)-F(a)$ .

הוכחה

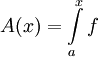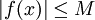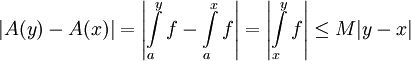כיוון ש-f אינטגרבילית ב- $[a,b]$ משפט 9 נותן שלכל $x\in[a,b]$ f אינטגרבילית בקטע $[a,x_0]$ ולכן $A(x)=\int\limits_a^x f$ מוגדרת היטב. נוכיח ש-A רציפה ע"י זה שהיא מקיימת את תנאי ליפשיץ. ובכן f אינטגרבילית ובפרט היא חסומה: $|f(x)|\le M$ לכל $x\in[a,b]$ . כעת אם $y>x\in[a,b]$ אז $|A(y)-A(x)|=\left|\int\limits_a^y f-\int\limits_a^x f\right|=\left|\int\limits_x^y f\right|\le M|y-x|$ ונובע ש-A רציפה. כעת נניח ש-f רציפה בנקודה $x_0\in[a,b]$ . ר"ל A גזירה שם. 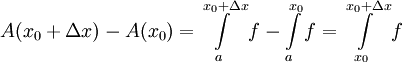ובכן $A(x_0+\Delta x)-A(x_0)=\int\limits_a^{x_0+\Delta x} f-\int\limits_a^{x_0} f=\int\limits_{x_0}^{x_0+\Delta x} f$ . 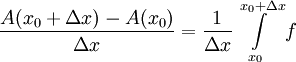מתקיים $\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f$ . 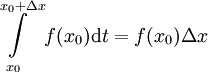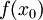נעיר ש- $\int\limits_{x_0}^{x_0+\Delta x} f(x_0)\mathrm dt=f(x_0)\Delta x$ (כי $f(x_0)$ פונקציה קבועה). לכן 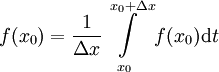$f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}f(x_0)\mathrm dt$ . מכאן ש- 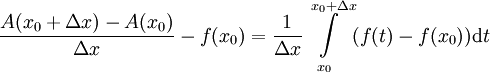$\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}(f(t)-f(x_0))\mathrm dt$ . נותר להוכיח שכאשר 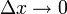$\Delta x\to0$ אגף שמאל (ולכן אגף ימין) שואף ל-0. לצורך זה יהי 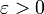$\varepsilon>0$ נתון. 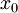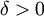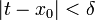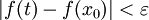כיוון ש-f רציפה ב- $x_0$ קיים $\delta>0$ כך שאם $|t-x_0|<\delta$ אז $|f(t)-f(x_0)|<\varepsilon$ . כעת נניח ש- 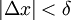$|\Delta x|<\delta$ . 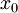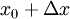אם כן האינטגרל באגף ימין הוא על קטע בין $x_0$ ל- $x_0+\Delta x$ ולכן כל t בקטע זה מקיים 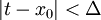$|t-x_0|<\Delta$ . נובע שלכל t בקטע 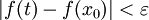$|f(t)-f(x_0)|<\varepsilon$ . יוצא שאם 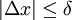$|\Delta x|\le\delta$ אז עיבוד הנוסחה נכשל (שגיאת תחביר): \left|\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)\right|=\left|\frac1{\Delta x}\int\limits_{x_0}^{x_0+\Delta x}(f(t)-f(x_0))\mathrm dt<\frac1{|\Delta x|}|\Delta x|\varepsilon

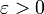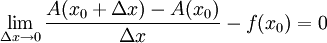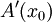. הדבר אפשרי לכל $\varepsilon>0$ . לכן $\lim_{\Delta x\to0}\frac{A(x_0+\Delta x)-A(x_0)}{\Delta x}-f(x_0)=0$ ז"א $A'(x_0)$ קיים ושווה ל- $f(x_0)$ . $\blacksquare$

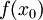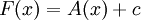נתון ש-f רציפה בכל $[a,b]$ . לפי החלק הקודם $\forall x\in[a,b]:\ A'(x)=f(x)$ , כלומר A קדומה ל-f ב- $[a,b]$ . קיים קבוע c כך ש- $F(x)=A(x)+c$ לכל $x\in[a,b]$ . מכאן ש-עיבוד הנוסחה נכשל (פונקציה \underbrac לא מוכרת): F(b)-F(a)=A(b)+c-(A(a)+c)=A(b)-A(a)=\int\limits_a^b f-\underbrac{\int\limits_a^a f}_{=0}

. $\blacksquare$

מסקנה

אם f רציפה בקטע $[a,b]$ אז קיימת לה פונקצייה קדוומה ב- $[a,b]$ .

הוכחה

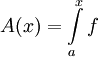כיוון ש-f רציפה בקטע $[a,b]$ כולו מתקיים $A(x)=\int\limits_a^x f$ קדומה ל-f ב- $[a,b]$ .

דוגמאות

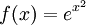$f(x)=e^{x^2}$ . זו פונקציה אלמנטרית ומוגדרת בכל 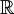$\mathbb R$ , ולכן רציפה שם. לפי המסקנה יש לה פונקציה קדומה. זו דוגמה קלאסית לפונקציה אלמנטרית שהפונקציה הקדומה שלה לא אלמנטרית.
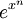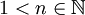
$e^{x^n}$ כאשר $1<n\in\mathbb N$
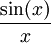
$\frac{\sin(x)}x$
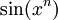
$\sin(x^n)$
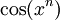
$\cos(x^n)$

תרגילים לחידוד

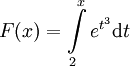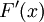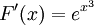
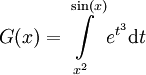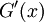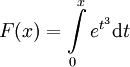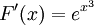נגדיר $F(x)=\int\limits_2^x e^{t^3}\mathrm dt$ . נמצא את $F'(x)$ : לפי חלק א של משפט 12 מתקיים $F'(x)=e^{x^3}$
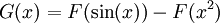נגדיר $G(x)=\int\limits_{x^2}^{\sin(x)} e^{t^3}\mathrm dt$ . נמצא את $G'(x)$ : נגדיר $F(x)=\int\limits_0^x e^{t^3}\mathrm dt$ ולכן $F'(x)=e^{x^3}$ לפי זה $G(x)=F(\sin(x))-F(x^2)$ ולכן, ע"פ כלל השרשרת,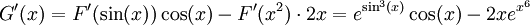 $G'(x)=F'(\sin(x))\cos(x)-F'(x^2)\cdot2x=e^{\sin^3(x)}\cos(x)-2xe^{x^6}$

גרף (1)

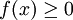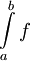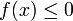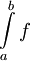הגדרה: עבור $f(x)\ge0$ רציפה ב- $[a,b]$ נגדיר את השטח שמתחת לגרף של f ע"י $\int\limits_a^b f$ . לפי זה, אם $f(x)\le0$ ב- $[a,b]$ אז $\int\limits_a^b f$ = מספר שלילי או 0 שהוא "מינוס השטח שמעל הגרף" (גרף (2)). אם f מחליפה סימן (גרף (3)) אז 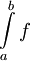$\int\limits_a^b f$ = השטח מעל ציר ה-x פחות השטח מתחת לצייר ה-x ולכן 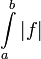$\int\limits_a^b |f|$ = השטח בין הגרף לציר ה-x.

דוגמת חישוב

גרף (4)

כאן ברור שהשטח בין הגרפים הוא 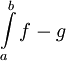$\int\limits_a^b f-g$ , ובנימוק פשוט זה נכון בכל מקרה ש- 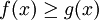$f(x)\ge g(x)$ ב- $[a,b]$ .

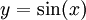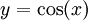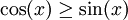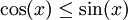למשל נחשב את השטח שבין הגרפים $y=\sin(x)$ ו- $y=\cos(x)$ בקטע $\left[0,\tfrac\pi2\right]$ גרף (5) תשובה: בקטע $\left[0,\tfrac\pi4\right]$ מתקיים $\cos(x)\ge\sin(x)$ ובקטע $\left[\tfrac\pi4,\tfrac\pi2\right]$ מתקיים $\cos(x)\le\sin(x)$ . לכן השטח הוא $\int\limits_0^\frac\pi4 (\cos(x)-\sin(x))\mathrm dx+\int\limits_\frac\pi4^\frac\pi2 (\sin(x)-\cos(x))\mathrm dx=[\sin(x)+\cos(x)]_{x=0}^\frac\pi4+[-\sin(x)-\cos(x)]_{x=\frac\pi4}^\frac\pi2=\frac\sqrt22+\frac\sqrt22-(0+1)=2\sqrt2-2$ .