83-112 חדו"א 1 להנדסה/נושאי הקורס

מבחנים מהעבר

• מבחן מועד א תשע"ו
  • פתרון
• מבחן מועד ב תשע"ו
• מבחן מועד ג תשע"ו
• מבחן דמה תשע"ו
  • פתרון
• מבחן לדוגמה תשע"ו
  • פתרון
• מבחן דמה תשע"ז
• מבחן מועד א' תשע"ז
  • פתרון מבחן מועד א' תשע"ז
• מבחן מועד ב' תשע"ז
• מבחן מועד ג' תשע"ז
• מבחן דמה תשע"ח
• מבחן מועד א' תשע"ח
  • פתרון מבחן מועד א' תשע"ח
• מבחן מועד ב' תשע"ח
• מבחן מועד ג' תשע"ח

נושאי ההרצאות

שימו לב: נושאי ההרצאות יעודכנו במהלך הסמסטר לפי קצב ההתקדמות בפועל.

הרצאה 1

• מבוא למספרים - טבעיים, שלמים, רציונאליים, ממשיים.
• שורש 2, 0.999.
• חזקות.
• לוגריתמים.
• מבוא לגבולות (שיטות אלגבריות: כפל בצמוד, הוצאת חזקה משמעותית).
  • [math]\displaystyle{ \lim_{x\to 2}\frac{x^2-4}{x-2} }[/math]
  • [math]\displaystyle{ \lim_{x\to\infty}\frac{2x^2+5x+3}{3x^2-100} }[/math]
  • [math]\displaystyle{ \lim_{x\to \infty}\sqrt{x^2+x+1}-x,\lim_{x\to \infty}\sqrt{x^2+1}-x }[/math]
  • [math]\displaystyle{ \lim_{x\to\infty}x^2-x }[/math]

הרצאה 2

• כמתים, שלילת כמתים.
• חסמים.

הרצאה 3

• ברציונאליים אין לכל קבוצה חסומה מלעיל חסם עליון.
• הגדרת הגבול של סדרה במובן הצר.

הרצאה 4

• גבול הוא יחיד.
  • נניח בשלילה שיש שני גבולות שונים. החל משלב מסויים כל איברי הסדרה גדולים מאמצע הקטע בין שני הגבולות וגם קטנים ממנו, בסתירה.
• הסדרה הקבועה.
• כל סדרה המתכנסת במובן הצר חסומה.
• אריתמטיקה (חשבון) גבולות.
  • (אי שיוויון המשולש.)
  • סכום.
  • מכפלה.
  • חלוקה (תרגיל לבית).

הרצאה 5

• התכנסות במובן הרחב.
• אחד חלקי 'שואפת לאינסוף' היא אפיסה, ההפך לא נכון.
• סנדביץ' וחצי סדנביץ'.
• [math]\displaystyle{ a_n\to 0 \iff |a_n|\to 0 }[/math]
• חסומה כפול אפיסה היא אפיסה.

הרצאה 6

• אינדוקציה.
• ברנולי - אקספוננט חיובי שואף לאפס, אחד או אינסוף.
• אריתמטיקה מורחבת (הכתיב הוא מקוצר ואינו מדוייק):
  • חסומה כפול אפיסה = אפיסה
  • חסומה חלקי אינסוף = אפיסה
  • [math]\displaystyle{ \infty+\infty=\infty }[/math]
  • [math]\displaystyle{ \infty\cdot\infty=\infty }[/math]
  • [math]\displaystyle{ \infty^\infty=\infty }[/math]
  • [math]\displaystyle{ \frac{1}{0}\neq\infty }[/math]
  • [math]\displaystyle{ \frac{1}{0^+}=\infty }[/math]
  • [math]\displaystyle{ 0^\infty = 0 }[/math]
  • אינסוף כפול סדרה השואפת למספר חיובי = אינסוף.
  • אינסוף כפול סדרההשואפת למספר שלילי = אינסוף.
  • יש גבול סופי + אין גבול סופי = אין גבול סופי.
  • אינסוף ועוד חסומה שווה אינסוף.
  • אם [math]\displaystyle{ a\gt 1 }[/math] אזי [math]\displaystyle{ a^\infty=\infty }[/math]
• המקרים הבעייתיים בהם צריך להפעיל מניפולציות אלגבריות או משפטים על מנת לחשב את הגבול:
  • [math]\displaystyle{ \frac{0}{0},\frac{\infty}{\infty},0\cdot\infty,\infty-\infty,0^0,\infty^0,1^\infty }[/math]
• מבחן המנה (ללא הוכחה).
• הגבול של השורש הn של n.

הרצאה 7

• סדרה מונוטונית וחסומה מתכנסת.
• המספר e.
• [math]\displaystyle{ 2\lt e\lt 4 }[/math].
• אם [math]\displaystyle{ a_n\to\infty }[/math] אזי [math]\displaystyle{ \left(1+\frac{1}{a_n}\right)^{a_n}\to e }[/math]
  • [math]\displaystyle{ [a_n]\leq a_n \leq [a_n]+1 }[/math], כאשר [math]\displaystyle{ [a_n] }[/math] הוא המספר השלם הגדול ביותר שקטן או שווה ל[math]\displaystyle{ a_n }[/math].
  • [math]\displaystyle{ \left(1+\frac{1}{[a_n]+1}\right)^{[a_n]}\leq\left(1+\frac{1}{a_n}\right)^{a_n}\leq \left(1+\frac{1}{[a_n]}\right)^{[a_n]+1} }[/math]
  • שני הצדדים שואפים לe ולכן לפי כלל הסנדוויץ הסדרה אכן שואפת לe.
• אם [math]\displaystyle{ a_n\to -\infty }[/math] אזי [math]\displaystyle{ \left(1+\frac{1}{a_n}\right)^{a_n}\to e }[/math]
  • ראשית [math]\displaystyle{ \left(1-\frac{1}{n}\right)^{n}\to \frac{1}{e} }[/math] (הוכחה בקישור לערך על המספר e).
  • כעת חזקה שלילית הופכת את השבר, וניתן לסיים את ההוכחה באופן דומה להוכחה במקרה הקודם.

• אם [math]\displaystyle{ a_n\to 1 }[/math] אזי [math]\displaystyle{ a_n^{b_n}\to e^{\lim b_n\cdot(a_n-1)} }[/math]
  • [math]\displaystyle{ a_n^{b_n}=\left[\left(1+(a_n-1)\right)^{\frac{1}{a_n-1}}\right]^{ b_n\cdot (a_n-1)} }[/math].
  • [math]\displaystyle{ \left(1+(a_n-1)\right)^{\frac{1}{a_n-1}}\to e }[/math] בין אם [math]\displaystyle{ a_n-1 }[/math] שלילי או חיובי, לפי הטענות לעיל.
  • שימו לב שאם [math]\displaystyle{ a_n=1 }[/math], אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב[math]\displaystyle{ a_n-1 }[/math] ששווה אפס.

• דוגמא:
  • [math]\displaystyle{ \lim\left(\frac{n+1}{n-2}\right)^n=e^{\lim n\cdot\left(\frac{n+1}{n-2}-1\right)}=e^{\lim\frac{3n}{n-2}}=e^3 }[/math]

הרצאה 8

• פונקציות וגבולות של פונקציות, לפי קושי ולפי היינה.

הרצאה 9

• הגדרת סינוס וקוסינוס ע"י מעגל היחידה.
  • [math]\displaystyle{ sin^2(x)+cos^2(x)=1 }[/math]
  • [math]\displaystyle{ sin(-x)=-sin(x),cos(-x)=cos(x) }[/math]
  • [math]\displaystyle{ sin(a+b)=sin(a)cos(b)+sin(b)cos(a),cos(a+b)=cos(a)cos(b)-sin(a)sin(b) }[/math]
  • [math]\displaystyle{ sin(2x)=2sin(x)cos(x),cos(2x)=cos^2(x)-sin^2(x) }[/math]

• 
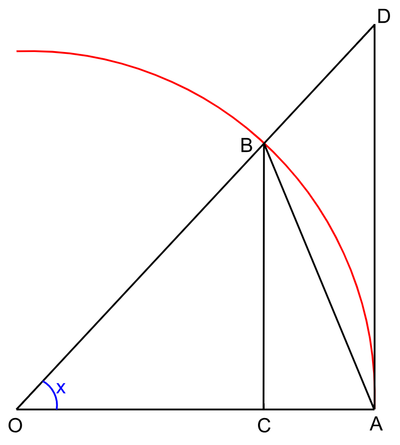
  • עבור זוית [math]\displaystyle{ 0\lt x\lt \frac{\pi}{2} }[/math] שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש:
  • [math]\displaystyle{ S_{\triangle AOB}\lt S_{\bigcirc AOB}\lt S_{\triangle AOD} }[/math]
  • [math]\displaystyle{ \frac{sin(x)}{2}\lt \frac{x}{2}\lt \frac{tan(x)}{2} }[/math]
    • כיוון ש[math]\displaystyle{ 0\lt sin(x)\lt x }[/math] בתחום [math]\displaystyle{ (0,\frac{\pi}{2}) }[/math], נובע לפי סנדוויץ' ש[math]\displaystyle{ \lim_{x\to 0^+}sin(x)=0 }[/math].
    • כיוון שמדובר בפונקציה אי זוגית, נובע שזה גם הגבול משני הצדדים.
    • כעת בתחום [math]\displaystyle{ (-\frac{\pi}{2},\frac{\pi}{2}) }[/math] הקוסינוס חיובית ולכן [math]\displaystyle{ cos(x)=\sqrt{1-sin^2(x)} }[/math] ונובע כי [math]\displaystyle{ \lim_{x\to 0}cos(x)=1 }[/math].
  • נחלק את אי השיוויון הטריגונומטרי בסינוס ונקבל:
  • [math]\displaystyle{ 1\lt \frac{x}{sin(x)}\lt \frac{1}{cos(x)} }[/math]
  • לפי כלל הסנדביץ [math]\displaystyle{ \lim_{x\to 0^+}\frac{sin(x)}{x}=1 }[/math]
  • כיוון שמדובר בפונקציה זוגית, נובע שהגבול משני הצדדים שווה 1.

• ראינו ש[math]\displaystyle{ \lim_{x\to 0}\frac{sin(x)}{x}=1 }[/math].
• שימו לב ש[math]\displaystyle{ \lim_{x\to\infty}\frac{sin(x)}{x}=0 }[/math], כיוון שמדובר בחסומה חלקי שואפת לאינסוף.

הרצאה 10

• תתי סדרות וגבולות חלקיים (ללא הוכחה)
  • סדרה מתכנסת לגבול אם"ם הגבול החלקי העליון והתחתון שווים לו.
  • אם ניתן לחלק סדרה לתתי סדרות שכולן מתכנסות לאותו גבול, אזי זה גבול הסדרה.
• מסקנה: גבול של פונקציה קיים בנקודה אם"ם הגבולות החד צדדיים קיימים ושווים לו.

• גבול של הרכבת פונקציות נכשל ללא רציפות.
  • [math]\displaystyle{ f(x)=\frac{x}{x}, g(x)=0 }[/math] מתקיים כי [math]\displaystyle{ \lim_{x\to 0}f(x)=1,\lim_{x\to 2}g(x)=0 }[/math] אבל [math]\displaystyle{ \lim_{x\to 2}f(g(x))\neq 1 }[/math].
• רציפות.
• טענה: אם f רציפה ב[math]\displaystyle{ x_0 }[/math] אזי לכל סדרה [math]\displaystyle{ x_n\to x_0 }[/math] (גם אם אינה שונה מ[math]\displaystyle{ x_0 }[/math]) מתקיים כי [math]\displaystyle{ f(x_n)\to f(x_0) }[/math].
• הרכבת רציפות: תהי f רציפה ב[math]\displaystyle{ x_0 }[/math] ותהי g רציפה ב[math]\displaystyle{ f(x_0) }[/math]. אזי [math]\displaystyle{ g\circ f }[/math] רציפה ב[math]\displaystyle{ x_0 }[/math].
  • הוכחה:
  • תהי סדרה [math]\displaystyle{ x_0\neq x_n\to x_0 }[/math] אזי [math]\displaystyle{ f(x_n)\to f(x_0) }[/math]
  • לפי הטענה הקודמת, [math]\displaystyle{ g(f(x_n))\to g(f(x_0)) }[/math].

• מיון אי רציפות.
  • רציפות - הגבול בנקודה שווה לערך בנקודה.
  • סליקה - הגבול קיים וסופי בנקודה, אך שונה מהערך בנקודה או שהפונקציה אינה מוגדרת בנקודה.
  • קפיצתית (מין ראשון) - הגבולות החד צדדיים קיימים סופיים ושונים בנקודה.
  • עיקרית (מין שני) - אחד הגבולות החד צדדיים אינו קיים או שאינו סופי.

הרצאה 11

הגדרת הנגזרת

• [math]\displaystyle{ f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h} }[/math]
• [math]\displaystyle{ \lim{h\to 0} \frac{f(x_0+h)-f(x_0)}{h} =\{h=x-x_0\} = \lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0} }[/math]
  • הסבר לגבי שיטת ההצבה בה השתמשנו לעיל:
  • נניח כי [math]\displaystyle{ \lim{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}=f'(x_0) }[/math] ונוכיח כי [math]\displaystyle{ \lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0) }[/math], והוכחה דומה בכיוון ההפוך.
  • תהי [math]\displaystyle{ x_0\neq x_n\to x_0 }[/math] נגדיר את הסדרה [math]\displaystyle{ 0\neq h_n=x_n-x_0\to 0 }[/math].
  • כיוון ש[math]\displaystyle{ \frac{f(x_0+h_n)-f(x_0)}{h_n}\to f'(x_0) }[/math] נובע כי [math]\displaystyle{ \frac{f(x_n)-f(x_0)}{x_n-x_0}\to f'(x_0) }[/math].
• אם f גזירה בנקודה, היא רציפה בנקודה:
  • צ"ל [math]\displaystyle{ \lim_{x\to x_0}f(x)=f(x_0) }[/math]
  • לפי אריתמטיקה של גבולות זה שקול ל [math]\displaystyle{ \lim_{x\to x_0}f(x)-f(x_0)=0 }[/math]
  • לפי עקרון win (קיצור של wouldn't it be nice?) מתקיים כי [math]\displaystyle{ \lim_{x\to x_0}f(x)-f(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\cdot (x-x_0)=f'(x_0)\cdot 0 = 0 }[/math]
• פונקציה הערך המוחלט אינה גזירה באפס
  • [math]\displaystyle{ (|x|)'(0) = \lim_{h\to 0}\frac{|h|-|0|}{h}=\lim\frac{|h|}{h} }[/math] וגבול זה אינו קיים, כיוון שהגבולות החד צדדים שונים.
  • ניתן לשים לב גם ש[math]\displaystyle{ |x|=\sqrt{x^2} }[/math], וכמו כן נראה בהמשך כי[math]\displaystyle{ \sqrt{x} }[/math] אינה גזירה באפס.

הנגזרות של הפונקציות האלמנטריות

• טריגו:
  • [math]\displaystyle{ \lim_{h\to 0}\frac{1-cos(h)}{h}=\lim_{h\to 0}\frac{sin^2(h)}{h(1+cos(h))}=\lim_{h\to 0}sin(h)\cdot \frac{sin(h)}{h}\cdot \frac{1}{1+cos(h)}=0\cdot 1 \cdot \frac{1}{2}=0 }[/math]
  • [math]\displaystyle{ (sin(x))'=\lim_{h\to 0}\frac{sin(x+h)-sin(x)}{h}=\lim_{h\to 0}\frac{sin(x)cos(h)+sin(h)cos(x)-sin(x)}{h}=\lim_{h\to 0}sin(x)\cdot \frac{cos(h)-1}{h} + cos(x)\cdot \frac{sin(h)}{h}=cos(x) }[/math]
  • באופן דומה [math]\displaystyle{ (cos(x))'=-sin(x) }[/math]
• לוג:
  • [math]\displaystyle{ \lim_{h\to 0}\frac{log(1+h)}{h}=\lim_{h\to 0}\frac{1}{h}\cdot log(1+h)=\lim_{h\to 0}log\left(\left(1+h\right)^{\frac{1}{h}}\right)=log(e) }[/math]
    • המעבר האחרון נובע מהעובדה שפונקצית הלוג רציפה.
    • (בפרט נובע כי [math]\displaystyle{ \lim_{x\to 0}\frac{ln(1+x)}{x}=1 }[/math].)
  • [math]\displaystyle{ (log(x))'=\lim_{h\to 0}\frac{log(x+h)-log(x)}{h}= \lim_{h\to 0}\frac{log\left(\frac{x+h}{x}\right)}{h}=\lim_{h\to 0}\frac{1}{x}\cdot\frac{log\left(1+\frac{h}{x}\right)}{\frac{h}{x}}=\frac{log(e)}{x} }[/math]
    • בפרט נובע כי [math]\displaystyle{ (ln(x))' = \frac{1}{x} }[/math]
• אקספוננט:
  • [math]\displaystyle{ \lim_{h\to 0}\frac{a^h-1}{h} = \{t=a^h-1, h=log_a(1+t)\} = \lim_{t\to 0} \frac{t}{log_a(1+t)} = \frac{1}{log_a(e)} = \frac{1}{\frac{ln(e)}{ln(a)}}=ln(a) }[/math]
  • [math]\displaystyle{ (a^x)' = \lim_{h\to 0}\frac{a^{x+h}-a^x}{h}= \lim_{h\to 0}a^x\cdot \frac{a^h-1}{h}=a^x\cdot ln(a) }[/math]
    • בפרט נובע כי [math]\displaystyle{ (e^x)'=e^x }[/math].
• חזקה:
  • [math]\displaystyle{ (x^\alpha)'=\alpha x^{\alpha-1} }[/math] לכל [math]\displaystyle{ \alpha\in \mathbb{R} }[/math], הוכחה בהמשך.
    • בפרט:
    • [math]\displaystyle{ (1)'=0 }[/math]
    • [math]\displaystyle{ (\frac{1}{x})' = (x^{-1})'=-\frac{1}{x^2} }[/math]
    • [math]\displaystyle{ (\sqrt{x})'=(x^{\frac{1}{2}})'=\frac{1}{2\sqrt{x}} }[/math]

הרצאה 12

• נוסחאות הגזירה.

הרצאה 13

• פונקציה הופכית, נגזרת של פונקציה הופכית.

הרצאה 14

• משפט ערך הביניים.
• תתי סדרות, גבול חלקי עליון ותחתון (כנראה ללא הוכחה).
• משפטי ויירשטראס.

הרצאה 15

• משפט פרמה.
• משפט רול.
• משפט לגראנז'.
• משפט לגראנז' המוכלל.

הרצאה 16

• כלל לופיטל (הוכחה לחלק מהמקרים).
• כיצד להעזר בלופיטל בכל אחד מהמקרים הבעייתיים.

הרצאה 17

• פולינום טיילור.
• שארית לגראנז' בפולינום טיילור.

הרצאה 18

• אינטגרל - מסויים ולא מסוים.
• הצגת נוסחאת ניוטון לייבניץ - הוכחה עם הערך הממוצע האינטגרלי.

הרצאה 19

• אינטגרציה בחלקים.
• שיטת ההצבה.

הרצאה 20

• אינטגרל על פונקציה רציונאלית.

הרצאה 21

• סכומי רימן.
• אורך עקומה, נפח גוף סיבוב.

הרצאה 22

• אינטגרלים לא אמיתיים.
• מבחני התכנסות.